Комплект оборудования:
|
Модель |
SP5600 |
DT5720A |
SP5601 |
SP5650C |
|
Описание |
Блок питания и усиления |
Настольный дигитайзер 250 Мвыб/с |
Драйвер светодиода (LED) |
Держатель сенсора для SP5600 с SiPM |
|
|
||||
Цель эксперимента:
Статистические свойства световых импульсов, испускаемых драйвером светодиода.
Основы эксперимента:
Спонтанное излучение света является результатом случайных распадов возбужденных атомов и, как ожидается, подчиняется распределению Пуассона. SiPM позволяет поимпульсно регистрировать количество падающих фотонов, что открывает возможность применять базовые навыки в области теории вероятностей и статистики при работе с квантами света, отображая спектр отклика SiPM на большой статистике импульсов.
Полученный спектр состоит из серии пиков, каждый из которых соответствует различному количеству сработавших ячеек. Каждый пик хорошо разделён и появляется с вероятностью, в первом приближении связанной с флуктуациями интенсивности света. В SiPM однородность отклика довольно высокая, однако из-за случайного распределения сработавших ячеек по чувствительной области детектора наблюдаются остаточные различия в усилении, что приводит к уширению пиков.
Ключевым элементом метода анализа является оценка площади под каждым пиком, что необходимо для восстановления функции плотности вероятности числа испущенных фотонов на импульс. Простой способ — рассматривать каждый пик как гауссовскую кривую. Таким образом, спектр, полученный в ответ на фотоны, падающие на сенсор, можно представить как наложение гауссовских функций, каждая из которых соответствует определённому количеству сработавших ячеек.
Бинное гауссовское распределение для Npk событий может быть записано следующим образом:
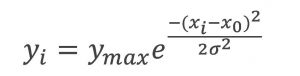
где yi — это количество событий в бине, центрированном на xi, а ymax — максимальное значение (высота пика), измеренное в x0. Поскольку Зная значение содержимого бина, центрированного в x0, и оценив стандартное отклонение σ\sigmaσ, можно определить общее число событий под пиком Npk..
Стандартное отклонение также можно просто рассчитать через ширину на полувысоте (FWHM), найдя положения бинов, в которых содержимое равно, получаемую путём поиска положения бинов, в которых содержимое равно ymax/2,при допущении, что FWHM = 2.355σ
Проведение эксперимента:
Подключите модуль SP5650A к одному из каналов блока SP5600 и соедините его аналоговый выход с каналом 0 дигитайзера DT5720A. Снимите защитные крышки с модулей SP5601 и SP5650A, нанесите оптическую смазку на оба конца оптического волокна и соедините их.
Установите на модуле SP5601 режим внутреннего триггера и подключите его триггерный выход ко входу “trigger IN” на DT5720A. Подключите модули к компьютеру через USB и включите питание устройств.
Используйте значения по умолчанию в программном обеспечении или оптимизируйте параметры для проведения эксперимента.
Блок-схема экспериментальной установки:
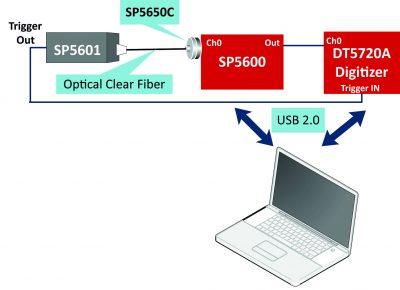 Результаты эксперимента:
Результаты эксперимента:
Функция плотности вероятности числа фотонов, испускаемых за один импульс, может быть оценена путём вычисления площади под каждым пиком в спектре. Для анализа статистической модели и среднего числа фотоэлектронов можно рассмотреть два различных подхода:
-
Независимая от модели оценка:
Среднее число фотонов определяется напрямую как среднее значение, рассчитанное по измеренному распределению без предположений о форме распределения.
-
Пуассоновская гипотеза :
Предполагается, что испускание фотонов подчиняется чистому распределению Пуассона. В этом случае среднее значение можно определить, используя вероятность P(0) — вероятность того, что ни одна ячейка не сработала (т.е. нет зарегистрированных фотоэлектронов).
Спектр фотоэлектронов, подтверждающий работу светодиодного источника, измеренный с использованием SiPM от Hamamatsu. Отдельные гауссовские пики, соответствующие различному числу сработавших ячеек, показаны красным цветом:
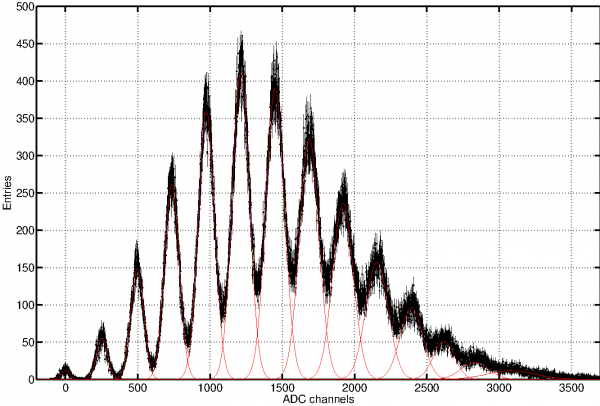
Данные светового спектра сопоставлены с простым пуассоновским распределением:
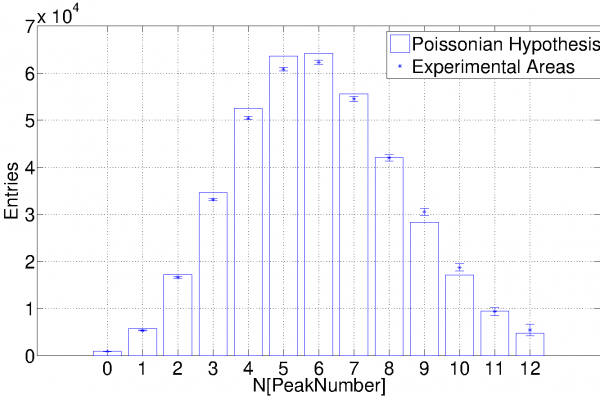
- Цена: Цену уточняйте



 Отправка с 11 мая 2026
Отправка с 11 мая 2026
