Учебный эксперимент: Распределение Пуассона и Гаусса

Комплект оборудования:

Цель эксперимента:

Изучение статистического распределения счётных скоростей гамма-радиоактивного источника. Сравнение полученных данных с распределением Пуассона, которое приближается к гауссовскому распределению при увеличении среднего числа отсчётов.

Основы эксперимента::

Количество зарегистрированных радиоактивных распадов за время Δt, как ожидается, подчиняется распределению Пуассона со средним значением μ. Это означает, что для данного радиоактивного источника вероятность того, что произойдут n распадов за заданный интервал времени Δt, определяется по формуле:

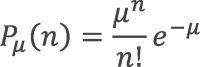
Где μ пропорционально размеру образца и времени измерения Δt, и обратно пропорционально периоду полураспада ​ T _1/2 нестабильного ядра. При увеличении значения μ, вероятность  P _μ (n) хорошо аппроксимируется гауссовским распределением:

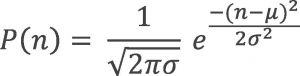
Где σ = √μ — это стандартное отклонение распределения.

Проведение эксперимента:

Установите модуль i-Spector digital на базу и поместите радиоактивный образец, например, кристалл LYSO, который предоставляется в качестве калибровочного источника. Включите питание i-Spector и подключите Ethernet-кабель. Подождите, пока температура стабилизируется (это может занять до получаса, по данным веб-интерфейса). Проверьте форму сигнала, при необходимости измените порог и ширину временного окна, затем запустите измерение энергетического спектра.

В качестве примера выполните 2-минутное измерение с образцом кристалла LYSO, установив соответствующее время накопления. Выберите область интереса (ROI) на пике 303 кэВ и зафиксируйте значение, указанное в области ROI. Повторите эксперимент несколько раз и запишите значение площади в ROI при каждом измерении.

Результаты эксперимента:

Изменяя окно счёта, активность источника или выбранную область интереса (ROI), количество зарегистрированных событий меняется, а функция плотности вероятности постепенно переходит от пуассоновской формы к гауссовской. Пользователь может поработать с полученными данными, выполнив их аппроксимацию и сравнив теоретические ожидания с экспериментальными результатами. Ниже представлены результаты, полученные при проведении 100 последовательных измерений, из которых первые 30 использовались для построения пуассоновского распределения.

Слева показано пуассоновское распределение (аппроксимация: y = p0* (p1 ^x /x!)*e ^-p1​), справа — гауссовское распределение (аппроксимация:   )